장르: 애초에 역경을 딛고 이룩하는 숭고한 사랑이란 없다. 그 역경 자체가 사랑이다.
프로그램 특징: 그 곳에서 살아남는 사랑이 어떤 모습으로 걸어오는지 기다려 보고 싶다.
-
 [빅데이터분석기사 필기] 전챕터 오답 위주 내용 정리0401분이진 단위 정리1비트 (bit)0 또는 1-1바이트 (Byte)8비트2³ × 1 (아니고, 정확히는 8bit)1킬로바이트 (KB)1,024 바이트2¹⁰1메가바이트 (MB)1,024 KB = 1,048,576 B2²⁰1기가바이트 (GB)1,024 MB2³⁰1테라바이트 (TB)1,024 GB2⁴⁰1페타바이트 (PB)1,024 TB2⁵⁰1엑사바이트 (EB)1,024 PB2⁶⁰1제타바이트 (ZB)1,024 EB2⁷⁰ HDFS(Hadoop Distributed File System)빅데이터를 저장하기 위해 "여러 서버에 분산 저장" 하는 개념. 여러 서버에 복제본을 저장하기 때문에 서버 하나가 고장나도 데이터 복원이 가능함.네트워크를 통해 여러 파일을 관리하고 저장NAS는 하나의 서버에 저장하는 개념GFS 아이디..
[빅데이터분석기사 필기] 전챕터 오답 위주 내용 정리0401분이진 단위 정리1비트 (bit)0 또는 1-1바이트 (Byte)8비트2³ × 1 (아니고, 정확히는 8bit)1킬로바이트 (KB)1,024 바이트2¹⁰1메가바이트 (MB)1,024 KB = 1,048,576 B2²⁰1기가바이트 (GB)1,024 MB2³⁰1테라바이트 (TB)1,024 GB2⁴⁰1페타바이트 (PB)1,024 TB2⁵⁰1엑사바이트 (EB)1,024 PB2⁶⁰1제타바이트 (ZB)1,024 EB2⁷⁰ HDFS(Hadoop Distributed File System)빅데이터를 저장하기 위해 "여러 서버에 분산 저장" 하는 개념. 여러 서버에 복제본을 저장하기 때문에 서버 하나가 고장나도 데이터 복원이 가능함.네트워크를 통해 여러 파일을 관리하고 저장NAS는 하나의 서버에 저장하는 개념GFS 아이디.. -
 [Excel] VBA로 데이터 자동화하기0304분- 인프런 '데이터 자동화(with VBA)' 배영자 님의 강의를 수강했습니다. 엑셀 자동화 코드를 만들어줄 수 있냐는 의뢰를 받았다. 지금 작업 방식은 년도별로 달라지는 데이터를 업데이트하기 위해 각 년도별 파일을 모두 하나하나 열어서, 해당하는 값을 찾고, 데이터 셀을 복사해서 가지고와 붙여넣는다고 하셨다. 분명 자동화하면 도움이 될 것이다. 나는 컴활 1급이 있지만 장롱 컴활이기에 따로 공부를 하면서 만들어보기로 했다. 지금 해야하는 일은 파일 간 데이터 이동이다. 하나의 시트에, 해당하는 년도별 데이터를 종합해 모아놓아야 나중에 업데이트할 때도 편리하다. 지금까지 알고 있는 지식으로는 파일을 모두 열어놓으면 데이터 공유가 가능하다고 알고 있었다. 근데 매번 2013~2023까지의 파일을 모두 열어..
[Excel] VBA로 데이터 자동화하기0304분- 인프런 '데이터 자동화(with VBA)' 배영자 님의 강의를 수강했습니다. 엑셀 자동화 코드를 만들어줄 수 있냐는 의뢰를 받았다. 지금 작업 방식은 년도별로 달라지는 데이터를 업데이트하기 위해 각 년도별 파일을 모두 하나하나 열어서, 해당하는 값을 찾고, 데이터 셀을 복사해서 가지고와 붙여넣는다고 하셨다. 분명 자동화하면 도움이 될 것이다. 나는 컴활 1급이 있지만 장롱 컴활이기에 따로 공부를 하면서 만들어보기로 했다. 지금 해야하는 일은 파일 간 데이터 이동이다. 하나의 시트에, 해당하는 년도별 데이터를 종합해 모아놓아야 나중에 업데이트할 때도 편리하다. 지금까지 알고 있는 지식으로는 파일을 모두 열어놓으면 데이터 공유가 가능하다고 알고 있었다. 근데 매번 2013~2023까지의 파일을 모두 열어.. -
[빅데이터분석기사 필기] 키워드 정리0227분데이터베이스 : 일정 구조에 맞게 조직화된 데이터의 집합데이터베이스의 특징공용 데이터: 여러 사용자가 서로 다른 목적으로 데이터 공동 이용통합된 데이터: 동일한 데이터가 중복되어 있지 않음저장된 데이터: 저장매체에 저장변화되는 데이터: 새로운 데이터 추가, 수정, 삭제에도 현재의 정확한 데이터 유지(무결성) 데이터 산업의 이해데이터 사이언스: 정형/비정형 데이터를 막론하고 데이터 분석(총체적 접근법)Analytics: 이론적 지식IT: 프로그래밍적 지식Business: 비즈니스적 능력Hadoop: 여러 컴퓨터를 하나로 묶어 대용량 데이터를 처리하는 오픈 소스 빅데이터 솔루션빅데이터 기술 및 제도빅데이터 플랫폼의 계층 구조소프트웨어 계층 : 데이터 수집 및 정제, 처리 및 분석, 사용자/서비스 관리플랫폼 ..
-
 파이썬 가상환경설정0107분1. 프로젝트 별로 가상환경을 따로 관리 - 라이브러리를 관리한다. 라이브러리끼리 의존성 때문에 버전 관리를 위함라이브러리 설치가 파이썬 pipe로 설치되지 않고 해당하는 폴더 밑으로 설치되도록 가상환경 설정2. pip install virtualenv 3. cd 원하는 폴더명python -m venv [생성할 가상환경 이름]4. 가상 환경 활성화 [folder명]/bin/activate- 비활성화는 deactivate이때 실행권한이 없으면 unrestricted 설정해줘야 함chmod +x ./scarapping/bin/activatewindow 기준 powershell에서 관리자 권한으로 set-excutionpolicy unrestrictedmac : source venv/bin/activate5..
파이썬 가상환경설정0107분1. 프로젝트 별로 가상환경을 따로 관리 - 라이브러리를 관리한다. 라이브러리끼리 의존성 때문에 버전 관리를 위함라이브러리 설치가 파이썬 pipe로 설치되지 않고 해당하는 폴더 밑으로 설치되도록 가상환경 설정2. pip install virtualenv 3. cd 원하는 폴더명python -m venv [생성할 가상환경 이름]4. 가상 환경 활성화 [folder명]/bin/activate- 비활성화는 deactivate이때 실행권한이 없으면 unrestricted 설정해줘야 함chmod +x ./scarapping/bin/activatewindow 기준 powershell에서 관리자 권한으로 set-excutionpolicy unrestrictedmac : source venv/bin/activate5.. -
 기계 학습 개요1017분기계학습(저자 오일석)을 참고했습니다.기계학습이란기계학습이란 기계를 학습시킨다는 맥락에서 여러 정의를 가진다. 기계가 주어진 데이터에 대해 올바른 분류, 예측이 가능하게끔 학습시키는 과정이다. 기계학습이란 훈련집합을 이용해 데이터 생성 과정을 역으로 추청하는 문제다.데이터 생성 과정이란, 샘플 x가 발생할 확률과 target y(결과)를 모두 알고 있는 상황을 말한다. 우리는 보통 샘플에 대해 결과값만 알거나 샘플만 가지고 결과값이 없다. 샘플이 어떠한 과정으로 데이터를 생성하는지 알면 모델은 정확한 데이터 예측 또는 가상 데이터 생성이 가능해진다.기계학습이란 훈련집합에 없는 새로운 데이터, 테스트 집합에 대해 높은 성능을 보장하는 프로그램을 만드는 것이다. 즉, 일반화하는 작업이다. 테스트 집합에 대해..
기계 학습 개요1017분기계학습(저자 오일석)을 참고했습니다.기계학습이란기계학습이란 기계를 학습시킨다는 맥락에서 여러 정의를 가진다. 기계가 주어진 데이터에 대해 올바른 분류, 예측이 가능하게끔 학습시키는 과정이다. 기계학습이란 훈련집합을 이용해 데이터 생성 과정을 역으로 추청하는 문제다.데이터 생성 과정이란, 샘플 x가 발생할 확률과 target y(결과)를 모두 알고 있는 상황을 말한다. 우리는 보통 샘플에 대해 결과값만 알거나 샘플만 가지고 결과값이 없다. 샘플이 어떠한 과정으로 데이터를 생성하는지 알면 모델은 정확한 데이터 예측 또는 가상 데이터 생성이 가능해진다.기계학습이란 훈련집합에 없는 새로운 데이터, 테스트 집합에 대해 높은 성능을 보장하는 프로그램을 만드는 것이다. 즉, 일반화하는 작업이다. 테스트 집합에 대해.. -
Linear/Polynomial Regression1013분기계학습 선형, 다항 회귀 모델 실습하기 # Linear Regression Model 2차원 평면 상 데이터에 대해 해당 데이터를 잘 표현할 수 있는 선형 회귀 모델1. Loading the dataset# Generate 2-dimensionalX = [rand() * i * 0.5 - 20 for i in range(0, 100)]y = [x ** 3 * 0.002 - x ** 2 * 0.005 + x * 0.003 + rand() * 5 for x in X] 2. 데이터셋을 trainset & testset로 나누고 분포 시각화# Data random shuffleidx = list(range(length(x)))random.shuffle(idx)# Split data for train/test ..
-
 [금융전략을 위한 머신러닝] NLP1010분# 자연어 처리: 파이썬 패키지1. NLTK가장 유명한 nlp 파이썬 라이브러리. 학습된 영어용 토크나이저 punkt 를 다운해 사용한다. 2. TextBlobNLTK 위에 빌드되는 테스트 처리 단순화 라이브러리3. spaCy단일 목적에 하나의 알고리즘만 제시하여 선택할 필요 없이 생산성에 집중할 수 있다. # 이론 및 개념텍스트 데이터를 전처리하고 텍스트를 통계적 추론 알고리즘에 입력하기 전에 예측 특성으로 표현 # 전처리1. 토큰화텍스트를 토큰이라고 하는 의미 있는 세그먼트로 분할하는 작업.> 세그먼트: 문장의 구성요소 (단어, 구두점, 숫자 등)- NLTK Punkt 2. 불용어 제거모델링에 값을 거의 제공하지 않는 매우 일반적인 단어를 어휘에서 제외''' from nltk.corpus impor..
[금융전략을 위한 머신러닝] NLP1010분# 자연어 처리: 파이썬 패키지1. NLTK가장 유명한 nlp 파이썬 라이브러리. 학습된 영어용 토크나이저 punkt 를 다운해 사용한다. 2. TextBlobNLTK 위에 빌드되는 테스트 처리 단순화 라이브러리3. spaCy단일 목적에 하나의 알고리즘만 제시하여 선택할 필요 없이 생산성에 집중할 수 있다. # 이론 및 개념텍스트 데이터를 전처리하고 텍스트를 통계적 추론 알고리즘에 입력하기 전에 예측 특성으로 표현 # 전처리1. 토큰화텍스트를 토큰이라고 하는 의미 있는 세그먼트로 분할하는 작업.> 세그먼트: 문장의 구성요소 (단어, 구두점, 숫자 등)- NLTK Punkt 2. 불용어 제거모델링에 값을 거의 제공하지 않는 매우 일반적인 단어를 어휘에서 제외''' from nltk.corpus impor.. -
 지도 학습: 회귀(시계열 모델)0924분학습 목표: 시계열 모델 개념, 금융 데이터에서 시계열 모델로 미래 가치 예측하는 방법, 시계열 모델과 지도 회귀 모델의 비교, 시계열 예측에 사용할 수 있는 딥러닝 모델(LSTM) - 다양한 시계열 및 머신러닝 모델의 적용과 비교 - 모델 및 결과 해석, 선형 대 비선형 모델의 잠재적 과적합과 과소적합의 직관적 이해 - 머신러닝 모델에 사용할 데이터 준비와 변환 - 모델 성능 향상을 위한 특성 선택과 엔지니어링 - 모델 성능 향상을 위한 알고리즘 튜닝, 예측을 위한 ARIMA (시계열 모델) 이해, 구현, 튜닝 - LSTM 같은 딥러닝 기반 모델이 시계열 예측에 어떻게 사용되는 지 이해 목표와 예측 변수 간의 관계를 모델링한다예측 변수란 금융에서 회귀 기반 지도 학습의 활용 사례- 투자 기회 예측: 자..
지도 학습: 회귀(시계열 모델)0924분학습 목표: 시계열 모델 개념, 금융 데이터에서 시계열 모델로 미래 가치 예측하는 방법, 시계열 모델과 지도 회귀 모델의 비교, 시계열 예측에 사용할 수 있는 딥러닝 모델(LSTM) - 다양한 시계열 및 머신러닝 모델의 적용과 비교 - 모델 및 결과 해석, 선형 대 비선형 모델의 잠재적 과적합과 과소적합의 직관적 이해 - 머신러닝 모델에 사용할 데이터 준비와 변환 - 모델 성능 향상을 위한 특성 선택과 엔지니어링 - 모델 성능 향상을 위한 알고리즘 튜닝, 예측을 위한 ARIMA (시계열 모델) 이해, 구현, 튜닝 - LSTM 같은 딥러닝 기반 모델이 시계열 예측에 어떻게 사용되는 지 이해 목표와 예측 변수 간의 관계를 모델링한다예측 변수란 금융에서 회귀 기반 지도 학습의 활용 사례- 투자 기회 예측: 자.. -
 트리 알고리즘0818분5.1. Decision Tree로지스틱 회귀로 와인 분류하기결정 트리이해하기 쉬운 결정 트리 모델5.2. 교차 검증과 그리드 서치검증 세트교차 검증하이퍼파라미터 튜닝최적의 모델을 위한 하이퍼파라미터 탐색5.3. 트리의 앙상블정형 데이터와 비정형 데이터랜덤 포레스트엑스트라 트리그레이디언트 부스팅히스토그램 기반 그레디언트 부스팅앙상블 학습을 통한 성능 향상info() > 누락된 값이 있으면 어떻게 하나요?결측치는 훈련 세트의 mean으로 채우거나 버리거나, 최선은 둘 다 해봐야 압니다. **훈련 세트의 통계값으로 테스트 세트를 변환한다는 사실을 잊지 마세요**> 훈련 세트의 평균값으로 테스트 세트의 누락값을 채워야 합니다. ??? 같은 통계 세트로 특성 변환하는 거지 훈련 세트가 영향을 주는 건 아니지 않..
트리 알고리즘0818분5.1. Decision Tree로지스틱 회귀로 와인 분류하기결정 트리이해하기 쉬운 결정 트리 모델5.2. 교차 검증과 그리드 서치검증 세트교차 검증하이퍼파라미터 튜닝최적의 모델을 위한 하이퍼파라미터 탐색5.3. 트리의 앙상블정형 데이터와 비정형 데이터랜덤 포레스트엑스트라 트리그레이디언트 부스팅히스토그램 기반 그레디언트 부스팅앙상블 학습을 통한 성능 향상info() > 누락된 값이 있으면 어떻게 하나요?결측치는 훈련 세트의 mean으로 채우거나 버리거나, 최선은 둘 다 해봐야 압니다. **훈련 세트의 통계값으로 테스트 세트를 변환한다는 사실을 잊지 마세요**> 훈련 세트의 평균값으로 테스트 세트의 누락값을 채워야 합니다. ??? 같은 통계 세트로 특성 변환하는 거지 훈련 세트가 영향을 주는 건 아니지 않..
이진 단위 정리
| 1비트 (bit) | 0 또는 1 | - |
|---|---|---|
| 1바이트 (Byte) | 8비트 | 2³ × 1 (아니고, 정확히는 8bit) |
| 1킬로바이트 (KB) | 1,024 바이트 | 2¹⁰ |
| 1메가바이트 (MB) | 1,024 KB = 1,048,576 B | 2²⁰ |
| 1기가바이트 (GB) | 1,024 MB | 2³⁰ |
| 1테라바이트 (TB) | 1,024 GB | 2⁴⁰ |
| 1페타바이트 (PB) | 1,024 TB | 2⁵⁰ |
| 1엑사바이트 (EB) | 1,024 PB | 2⁶⁰ |
| 1제타바이트 (ZB) | 1,024 EB | 2⁷⁰ |
HDFS(Hadoop Distributed File System)
빅데이터를 저장하기 위해 "여러 서버에 분산 저장" 하는 개념. 여러 서버에 복제본을 저장하기 때문에 서버 하나가 고장나도 데이터 복원이 가능함.
- 네트워크를 통해 여러 파일을 관리하고 저장
- NAS는 하나의 서버에 저장하는 개념
- GFS 아이디어를 보고 만든 파일 시스템으로 비슷한 원리
- 분산 데이터베이스
- x86 서버의 CPU, RAM을 사용하므로 장비 증가에 따른 성능 향상이 용이하다 > 고성능 서버 대신 일반 컴퓨터 여러 대를 묶어 사용
- 네임노드와 네임노드 데이터는 다른 저장공간에 저장
- 네임노드는 실제 파일이 아닌 위치 정보 기억하는 서버: 파일 이름, 블록 위치, 복제 정보
- 네임노드 데이터는 네임노드가 기억하는 정보? 지도처럼 생긴 데이터
개인정보 비식별화
- 데이터 마스킹
- 이름: 김민지 → *** : 보호가 목적
개인정보 비식별화 기술에서 안전하게 데이터를 활용하도록 고안한 개념들
- k-Anonymity
- 최소 k명 이상이 같은 정보로 보여야 개인을 알 수 없게 만든다: 혼자 튀지 않게 만드는 기술: 범주화 등
- i-Diversity
- 같은 범주에서 i 개 이상의 민감 정보가 있어야 안전하다.
- “30대 남성 5명” 모두 질병 = 암이라면? → 누군지 몰라도, 그 사람들 모두 암이라는 걸 알아버림 ❌
- 가명처리 (Pseudonymization)
- 이름: 김민지 → 사용자001: 재식별 가능, 분석 가능, 법적으로는 여전히 개인정보 취급
- 범주화 (Generalization)
- Differential Privacy(개인정보 차등 보호)
- 개인이 포함되었는지 아닌지 알 수 없도록 수학적으로 보호: 분석 결과가 거의 바뀌지 않도록 ’노이즈(잡음)’를 살짝 섞는 것
- 노이즈란, 우연을 의미
데이터 처리
디스크에서 데이터 처리를 하냐 메모리(RAM)에서 처리하냐.
- 인메모리 기반
- 데이터를 메모리에 올려 작업하므로 빠름
- Spark
- 디스크 기반
- 느리지만 처리 단계마다 디스크 저장 -> 안정적
- Mapreduce - Hadoop에서 이용
빅데이터 탐색
대푯값, 기하평균, 변동률, 변동계수, 분산
🔹 변동률 (Growth Rate)
• 예: “매출이 작년보다 몇 % 늘었어?” → 비율 변화
• 여러 기간의 변동률이 있을 때, 단순 평균(X) 대신 기하 평균(√, ∛ 등) 사용!
🔹 왜 기하 평균을 쓰냐면: 변동률은 곱셈 관계이기 때문!
• 예: 1년 차 매출 증가율: +10% → ×1.10
• 2년 차 매출 감소율: -20% → ×0.80
전체 평균 증가율은 (1.10 × 0.80)¹ᐟ² = √0.88 ≈ 0.938 → 평균적으로 6.2% 감소
✅ 변동률의 대표값(평균)을 구할 땐 기하평균 이용
🔹 변동계수 (Coefficient of Variation, CV)
👉 데이터의 상대적인 변동성을 나타내는 지표
CV = (표준편차 / 평균) × 100
• 단위가 없어서 서로 다른 단위를 가진 데이터끼리도 비교 가능
• 표준편차 = √분산 그래서 CV는 결국 (√분산) ÷ 평균 즉, 분산과 밀접한 관련. CV가 높다는 건 분산도 크거나 평균이 작다는 뜻
📌 요약 정리
| 개념 | 대푯값 | 관련 | 개념 설명 |
|---|---|---|---|
| 변동률 | 기하 평균 | 곱셈 관계 | 연평균 성장률 계산에 적합 |
| 변동계수(CV) | 평균 기준으로 표준편차 해석 | 분산, 표준편차 | 데이터의 상대적 변동성 판단 |
| 📌 변동성(흔들림)을 나타내는 대표적인 척도들: | ||
|---|---|---|
| 이름 | 설명 | 이상치 영향 |
| 분산 | 값들이 평균에서 얼마나 퍼졌는지 (제곱 기준) | 영향 큼 |
| 표준편차 | 분산의 제곱근 | 영향 큼 |
| 사분위범위(IQR) | Q3 − Q1 (중간 50% 범위) | 영향 적음 ✅ |
| 변동계수(CV) | 표준편차 ÷ 평균 (상대적 흔들림) | 평균 작으면 민감함 |
선형 관계 회귀선 선형 회귀의 차이
- 선형 관계는 비례, 반비례로 해석할 수 있는 선, 관찰 결과(산점도)에서 직선 방향을 보고 결정
- 상관계수(correlation coefficeint, r) : 양음의 정도를 [-1~+1]로 표현
- 선형 회귀에서 상관계수의 제곱으로 결정계수(R²) 이용
- 회귀선(Regression)은 데이터 점을 설명하는 예측용 직선
- 선형 회귀는 선형 관계가 있다고 보고 회귀선을 수학적으로 찾는 과정
데이터 산점도 관찰
↓
선형 관계가 보인다?
↓
선형 회귀를 수행
↓
회귀선 도출 (예측 공식 y = ax + b)
- 결정계수는 설명 변수가 결과에 얼마나 영향을 주는지 보여주는 점수다.
Feature Scaling
Normalization vs Standardization

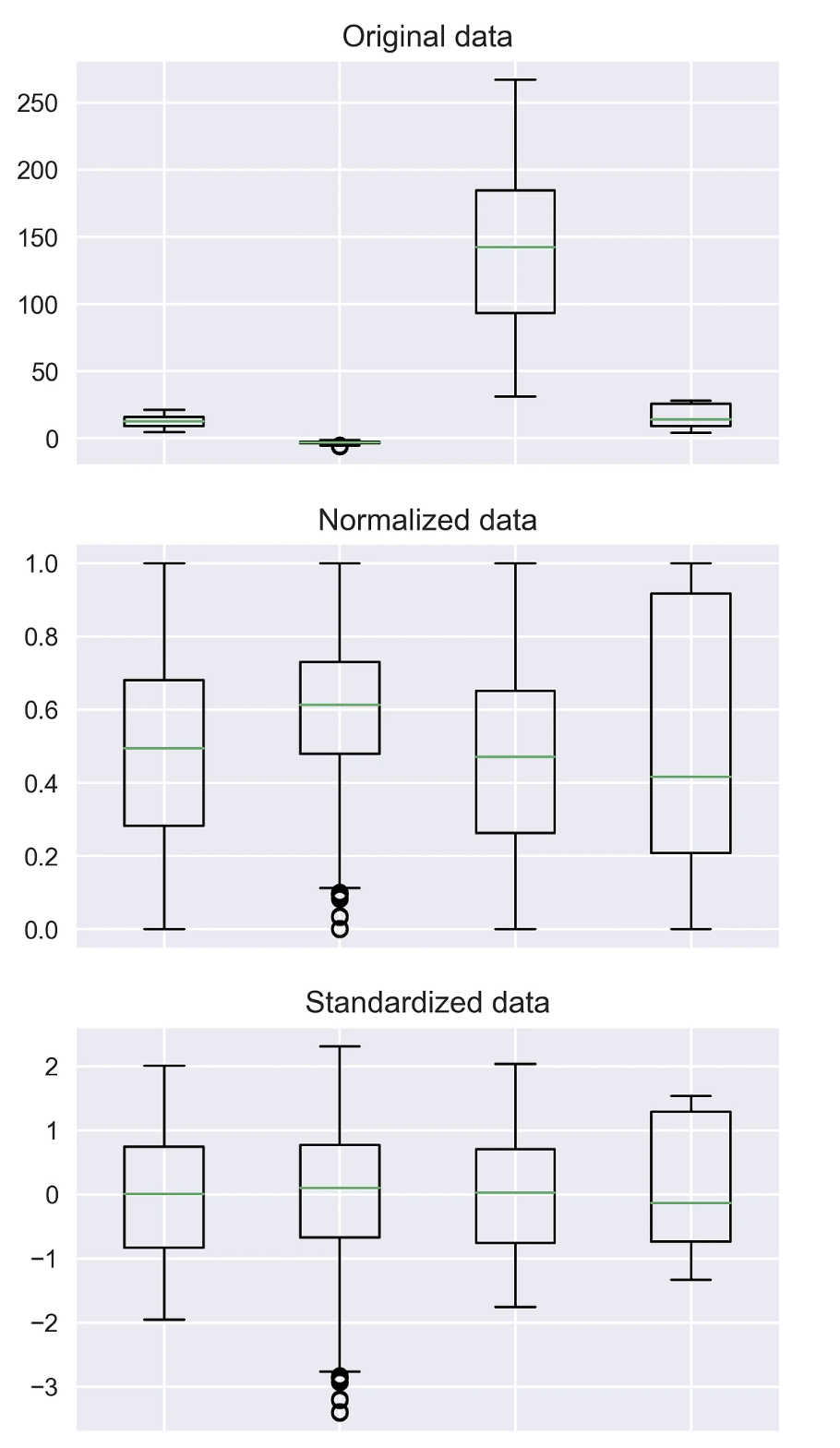
언제 정규화를 하고 언제 표준화를 할까?
명확한 답은 없다.
통상적으로는 표준화를 통해 이상치를 제거하고,
그 다음 데이터를 정규화 해 상대적 크기에 대한 영향력을 줄인 다음 분석을 시작한다고 한다.
출처)
[통계] 정규화(Normalization) vs 표준화(Standardization)
ML을 공부하는 사람이라면 feature scaling이 얼마나 중요한 지 알것이다. scikit-learn에는 많은 스케일링 메서드들이 모듈화 되어있는데, 기본적으로 정규화와 표준화가 무엇인지 이해해야 과제를 수
heeya-stupidbutstudying.tistory.com
앙상블 기법
Bootstrap
Bagging (Bootstrap Aggregating)
Boosting
Stagging
혼동 행렬
현실과 모델이 가지는 True / False , Positive / Negative 의 조합으로 혼동 행렬을 작성한다. 이때 TF / Positive - Negative의 의미만 통일해서 기억하면 이해하기 쉬워진다.
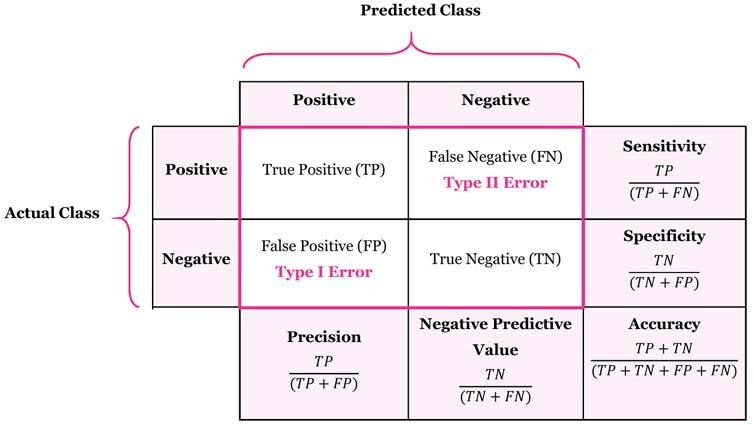
- FN
- 모델은 Negative로 예측했는데 Actual Class : Positive 이므로 틀렸다. False Negative 는 틀린 부정 == 실제론 Positive인데 Negative로 잘못 예측한거다.
- FP ? False Positive. 틀린 긍정 : 실제론 부정인데 긍정으로 잘못 예측했다.
- TP ? 참된 긍정. 긍정으로 예측했고, 사실이다.
- TN ?
| 특이도 (Specificity) | TN / TN+FP | 실제로 부정인 범주 중에서 모델이 부정을 맞게 예측한(TN)한 비율 -> 모델이 부정 / 실제로 부정값 |
| 민감도 (Sensitivity) | TP / TP+FN | 실제로 긍정인 범주(TP+FN) 중에서 긍정을 올바르게 예측(TP)한 비율 -> 모델이 긍정 / 실제로 긍정 |
| 거짓 긍정률 (FP Rate) | FP / TN+FP | 실제로 부정인 범주(TN+FP) 중에서 긍정으로 잘못 예측(FP)한 비율 -> 모델이 부정을 긍정으로 예측할 비율 |
| 정밀도 (Precision) | TP / TP+FP | 모델이 긍정으로 예측한 비율(TP+FP) 중에서 실제로 긍정(TP)인 비율 -> 모델이 긍정 / 사실일 비율 |
| 정확도 (Accuracy) | TP+TN / TP+TN+FP+FN | 전체 예측(TP+TN+FP+FN)에서 실제로 긍정 또는 부정으로 올바르게 예측한 것(TP+TN)이 차지하는 비율 -> 모델이 전체 예측에서 긍/부정을 맞춘 비율 |
| 오차비율 (Error Rate) | FP+FN / TP+TN+FP+FN | 전체 예측(TP+TN+FP+FN)에서 잘못 예측한 것(FP+FN)이 차지하는 비율 |
빅데이터분석기사 필기 오답노트 - 4과목(빅데이터 결과 해석)
빅데이터분석기사 필기 오답노트 - 4과목(빅데이터 결과 해석)
velog.io
데이터 시각화
예시를 쌍으로 외워서 어떤 상황에 쓰는지 암기해야 한다.
| 시각화 종류 | 방법 | 예시 |
|---|---|---|
| 분포 시각화 | 전체에서 부분 간 관계를 설명하는 방법 | 파이 차트 기법, 도넛 차트 기법, 트리 차트 |
| 관계 시각화 | 집단, 다변량 간의 상관관계를 확인하여 다른 수치의 변화를 예측하는 방법 | 산점도 기법, 버블 차트 기법, 히스토그램 기법 |
| 비교 시각화 | 히트맵 기법, 평행 좌표 그래프 기법, 체르노프 페이스 기법, 스타 차트 | |
| 공간 시각화 | 등치선도 기법, 도트맵 기법, 카토그램 기법 | |
| 시간 시각화 | 시간 흐름에 따른 변화를 통해 경향 파악 | 막대그래프 기법, 점그래프 기법 |
시각화 툴
Data Wrapper과 Chart Block의 차이
코딩 없이? 시각화, 웹 기반 보다는 데이터 래퍼는 사용자 목적에 따라 제작할 수 있는 레이아웃을 제공하여 데이터 변환의 느낌이고, 차트 블록은 데이터 베이스 형태의 데이터에 대해 차트를 웹 구현하는 것에 초점을 둔 툴이다.
👇 이 분 블로그 완전 강추
[빅데이터분석기사 필기 요약] IV.빅데이터 결과 해석 - 02. 분석 결과 해석 및 활용 (1)
빅데이터분석기사 필기 요약🔑 데이터시각화/ 시간시각화/ 분포시각화/ 관계시각화/ 비교시각화/ 공간시각화/ 시각화도구/ 태블로/ 인포그램/ 차트블록/ 데이터래퍼/ 비즈니스
sy-log.tistory.com
분석 모형 평가
우선, 모수 vs 비모수 검정을 알아야 한다. 모수 검정은 “모집단이 정규분포다”처럼 분포 모양을 가정하고 표본으로 검정하는 방법, 비모수 검정은 분포 모양을 가정하지 않고 순위, 빈도로 검정하는 방법을 말한다.
모수 검정을 위해선, 표본에 대해 정규성 만족 검정을 해야 한다. 정규성을 만족했으면 등분산 검정이 필요하다. 독립성 T검정
- 등분산 검정은 변수가 동일한 분산을 가지는 것을 말한다.
- 정규성(Shapiro-Wilk, K-S, Q-Q Plot) -> 등분산 ->
비모수 검정의 경우, 독립성 T 검정의 대응으로 만위트니 U 검정이 있다.
👇 심화학습용
[통계] 가설 검정 공부하기 1(모수 vs 비모수)
들어가기 전에 최근 ADP 실기 시험을 준비하면서 통계분석과 기계학습에 대해서 차근차근 다시 공부해보고 있는 와중에 처음 들어보는 검정 방법을 알게 되면서 이 글을 작성하게 되었습니다.
sooho-kim.tistory.com
👇 요약
[빅데이터분석기사 필기 요약] IV.빅데이터 결과 해석 - 01. 분석 모형 평가 및 개선 (3)
빅데이터분석기사 필기 요약🔑 모집단평균/ Z-검정/ T-검정/ 분산분석/ 모집단분산/ 카이제곱검정/ F-검정/ 적합도검정/ 정규성검정/ 샤피로-윌크 검정/ 콜모고로프-스미르노프 검정(K-S검
sy-log.tistory.com
가설 검정(Test)
각각의 검정은 통계 방법(알고리즘)으로 검정 결과로 나오는 p-value로 귀무가설의 채택, 기각을 정의한다.
- “검정 통계량”이라는 숫자를 계산해 그게 특정 분포에서 어디쯤에 있는지(p-value)를 보고 판단
| 검정 분류 | 상황 | 검정 | 사용하는 분포 |
|---|---|---|---|
| 모집단 평균 비교 | 평균 비교 (σ O) | Z-검정(n이 클 때) | Z-분포 (표준정규분포) |
| 평균 비교 (σ X) | t-검정 (소표본이거나 표준 편차 모를 때 표본으로 추정) |
t-분포 :Z와 비슷하지만 꼬리가 두꺼움 (표본 작을수록 더 퍼짐) | |
| 같은 집단의 전후 비교 | 대응표본 t-검정 | ||
| 두 집단 평균 비교 | 독립표본 t-검정 | ||
| 모집단 분산 비교 | 분산 비교 | F-검정(분산 간 비율), ANOVA, 카이제곱 | F-분포, χ²(카이제곱) 분포 |
| 적합성 검정 | 분포 적합 확인 | 카이제곱 적합도 검정 | |
| 정규성 검정 | 정규성 확인 | Shapiro-Wilk, K-S, Q-Q Plot, Anderson-Darling | |
| 변수 관계(독립성) 검정 | 범주형 독립성 | 카이제곱 독립성 검정, Fisher 검정 | |
| 비모수 검정 | 정규성 없는 경우 | 윌콕슨, 크루스칼-왈리스 검정(ANOVA의 비모수 대체) |
각 분포 별 차이
- Z분포: 기준이 되는 정규분포
- t분포: 작은 표본용 정규분포 - √(카이제곱 / 자유도)
- 카이제곱 분포: 정규분포 제곱합 - 항상 0이상이고 한 쪽으로 치우침
- F분포: 두 개의 카이제곱 분포끼리 나눈 값(비율) - 분산끼리 비교용(ANOVA)
정규 분포(Z) 기반. 카이제곱 -> t -> F 분포 로 변형, 조합해서 만든 검정용 분포.
- T-검정은 두 집단 간의 평균을 비교하는 모수적 총계 방법으로써 표본이 정규성, 등분산성, 독립성 등을 만족할 경우 적용
- (기출 선지) 카이제곱 검정은 범주형 변수가 정규 분포라면, 관찰한 빈도가 실제 기대한 이론적인 빈도로부터 유의미한 차이를 가지는지를 관찰하는 검증이다
- 예) “과일 선호도는 세 과일이 똑같이 인기 있을 것이다” → 기대값 = 20명. 근데 실제로는 [20, 15, 25]가 나왔어!
갑자기 지피티가
'❌ 카이제곱은 정규분포랑은 관련 없어!• 카이제곱 검정은 정규성 가정 안 함
• 분산 검정이라기보다, 빈도 데이터가 기대와 다른지를 보는 적합도 검정/독립성 검정이야'
라네. 기출 선지에서 '정규 분포라면'은 뭐지???
???? 카이제곱이 대체 뭔데 ㅠㅠ
카이제곱 검정은 범주형 데이터의 두 변인간의 상관성을 확인하기 위해 쓰이는 게 공통 구조
| 검정 목적 | 검정 이름 | 사용 데이터 | 비교 대상 | 대상 예시 |
| ① 분포 적합도 확인 | 적합도 검정 (Goodness of Fit) |
범주형 | 관측값 vs 이론적 분포 | 주사위가 공정한가? (각 면이 1/6인지) |
| ② 변수 간 관계 확인 | 독립성 검정 (Test of Independence) |
범주형 × 범주형 | 관측값 vs 기대값(독립일 때의 값) | 성별과 커피 선호가 관련 있나? |
| ③ 단일 모집단의 분산 추정 | (특수한 경우의 분산 검정) | 수치형 | 표본 분산 → 모분산 추정 | 제품 불량률이 기준 분산(4)과 같은가? (자주 안 씀) |
블로그를 읽으면 읽을수록 혼란이 가중되어 정리를 포기할까 하다가 . . 다행히ㅜㅜ 전문적으로 보이는 정리된 블로그를 찾았다
👇 전문적임 강추
카이제곱 분포와 검정 - 공돌이의 수학정리노트 (Angelo's Math Notes)
angeloyeo.github.io
요약: 카이제곱 분포는 모집단의 error 혹은 편차(deviation) 분석에 도움을 받을 수 있는 분포다.
카이제곱하면 자유도를 빼고 말할 수 없다. 자유도란 선택할 수 있는 변수(샘플)의 개수를 말한다.

위 블로그를 참고하면, 이렇게 정규분포에서 샘플을 뽑아 제곱해서 더한다. 그럼 항상 0보다 큰 값으로 그래프가 그려진다. 여기선 3개를 뽑았으니 자유도 3이다. 히스토그램 카운트란 제곱합을 여러 번해서 나온 히스토그램을 토대로 하나의 그래프를 뽑는 과정을 말한다.
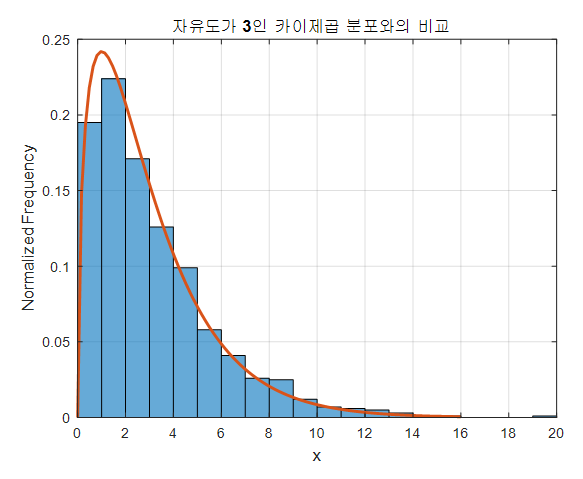
y축이 빈도를 나타내고, x축은 제곱합이므로 0 이상으로만 정의된다. 여기서 자유도(샘플의 개수)가 많아질수록, 중심극한 정리에 의해 정규분포에 가까워진다.
- 중심극한정리: 독립인 확률 변수들의 시행이 엄청많아지면 평균의 분포가 정규분포에 수렴
그런데 꼭 제곱해서 합하는 이유는 뭘까?
이를 이해하기 위해 오차를 정규분포로 설계하는 것을 이해해야 한다. 오차의 분포가 정규분포를 따르게 될 때, 카이제곱 분포를 이용하면 이 오차 혹은 편차가 우연히 발생한 수준인지 아닌지를 판별할 수 있게 된다.
독립성 검정 vs 분산 검정 vs 교차 분석
| 독립성 검정 (Independence Test) | 분산 검정 (Variance Test) | 교차 분석 |
| 📌 대표: 카이제곱 독립성 검정 주의할 점은 범주형 변수(남성, 여성)을 이용했다는 것이다. |성별 | 라면| 불호| 총계| | --- | --- | --- | --- | | 남자 | 30 | 20 | 50 | | --- | --- | --- | --- | | 여자 | 20 | 30 | 50 | “성별과 라면 취향 사이에 관계가 있을까?” 이럴 때 → 독립성 검정 사용! • 귀무가설: “성별과 취향은 무관하다” → p값 작으면 → “성별이 라면 선호도에 영향 있음“이라고 말할 수 있음 |
📌 대표: F-검정 (두 집단 분산 비교) • Levene 검정 (비모수 버전) 🎯 예시: • A반 수학 점수: [70, 72, 69, 71] → 분산이 작음 (점수 비슷함) • B반 수학 점수: [60, 80, 65, 85] → 분산이 큼 (점수 들쭉날쭉) • 귀무가설: “두 집단의 분산은 같다” → p값 작으면 → “분산 다름!” |
목적: 두 범주형 변수 간 연관성 확인 예를 들면, 음식 메뉴별로 성별 간 선택의 차이를 보이는지, 혹은 각 성별 별로 메뉴 선택의 차이를 보이는지 알아보기 위함이다. 해당하는 자유도에서 우리가 구한 카이제곱 통계량의 값이 더 작다면 성별 및 메뉴판에 대해 기댓값에서 유의하게 벗어나지 않는 다는 것을 알 수 있다. |
적합도 검정과 정규성 검정
적합도 검정은 주로 카이제곱 검정을 의미하고, 정규성 검정(정규분포를 따르는지)는 샤피로-윌크 검정, K-S 검정, Q-Q Plot을 이용
| 적합도 검정 | 정규성 검정 | |
|---|---|---|
| 목적 | 분포가 특정 이론(포아송, 이항 등)을 따르는지 확인 | 정규분포를 따르는지 확인 |
| 대표 기법 | 카이제곱 검정 | 샤피로-윌크, K-S 검정, Q-Q Plot 등 |
| 데이터 형태 | 주로 범주형, 빈도 데이터 | 주로 연속형 데이터 |
- 카이제곱 검정에서는 R 언어에서 chisq.test() 함수를 이용하여 나온 결과의 p-value 값이 0.05보다 클 경우 관측된 데이터가 가정된 확률을 따른다고 할 수 있다. == 귀무가설 기각
[빅데이터분석기사 필기] 적합도 검정 개념 및 기출문제
적합도 검정 적합도 검정은 표본 집단의 분포가 주어딘 특정 이론을 따르고 있는지를 검정하는 기법이다. 적합도 검정은 가정된 확률이 정해진 경우와 아닌 경우로 유형을 분리할 수 있다. 적합
ohaengsa.tistory.com
비즈니스 기여도 평가
| 항목 | 약어 | 설명 |
|---|---|---|
| 총 소유 비용 | TCO (Total Cost of Ownership) |
처음 살 때부터 고장·유지·운영까지 총 얼마 드는지 전부 계산 #연관비용 #주어진기간 |
| 투자 대비 효과 | ROI (Return on Investment) | 투자해서 얼마 벌었는지, 비율로 따져보는 수익률 #투자타당성 |
| 순 현재가치 | NPV (Net Present Value) | 앞으로 벌 돈(투자액-매출액)을 지금 가치(이자율)로 따져봤을 때 이득이냐 손해냐 #특정시점 #이자율 |
| 내부 수익률 | IRR (Internal Rate of Return) | 돈을 넣었을 때 연평균 몇 % 수익 나는 셈인지 계산하는 숫자 #NPV를 0으로 만드는 할인율 #연단위 |
| 투자 회수 기간 | PP (Payback Period) | 들인 돈을 다 회수하는 데 걸리는 시간 (예: 투자비 다 뽑는 데 2년 걸림) #누계 투자금액의 합 == 매출금액의 합 #흑자전환시점 |
- 'NPV = 0' 의 의미는 투자해서 앞으로 벌 돈과 들인 돈이 같은 수준.
- > 0이면 이익
- 이자율(Interest Rate) : 미래에 얼마나 벌 수 있을지 계산 - 수익률
- 할인율(Discount Rate) : 미래 돈을 현재 가치로 변환 - 현재 가치 분석
'Data Science > 자격증 공부' 카테고리의 다른 글
| [빅데이터분석기사 필기] 키워드 정리 (4) | 2025.02.27 |
|---|---|
| [ADsP] 군집분석 (0) | 2024.08.06 |
| [ADsP] 분석 거버넌스 체계 수립 (5) | 2024.08.05 |
| [ADsP] 용어 정리 (0) | 2024.08.05 |
| [ADsP] 주성분 분석 (3) | 2024.08.05 |



