장르: 애초에 역경을 딛고 이룩하는 숭고한 사랑이란 없다. 그 역경 자체가 사랑이다.
프로그램 특징: 그 곳에서 살아남는 사랑이 어떤 모습으로 걸어오는지 기다려 보고 싶다.
관계 대수 relational algebra
원하는 데이터를 어떠한 연산과 연산 순서로 가져오라고 명시하는 절차적인 언어. SQL의 이론적인 기초가 되는 언어다.
관계 DBMS는 SQL 질의를 DBMS 내부에서 관계대수식으로 변환한 후 최적의 질의 수행 계획을 찾는다.
우리는 DB에 SQL로 어떤 데이터를 달라고 명령하게 된다. 이 명령을 DBMS는 관계대수식으로 변환해서 연산을 수행하니 관계대수식을 알면 데이터 처리 방법에 대해 이해할 수 있다.
관계 데이터 모델에서 지원하는 두 가지 정형적인 언어
정형적인이 무슨 뜻 일까?
- 관계 해석 relational calculus
- 원하는 데이터만 명시
- 관계 대수 relational algebra
필수 관계 연산자
Selection σ

- selection의 조건을 predicate(술어)라고 한다.
- 조건에는 애튜리뷰트, 상수, 비교 연산자 등의 bool 연산자를 포함할 수 있다.
- 중복 튜플이 존재할 수 없다.
Projection π
- 릴레이션 애튜리뷰트의 부분 집합; 결과에 쓸 컬럼을 쓰면 된다; 중복 튜플이 존재할 수 있다.

집합 연산자
- UNION(∪), INTERSECTION(∩), DIFFERENCE(-)
여기서 교집합만 유도 연산자다.
- | 합집합 호환
두 릴레이션은 서로 같은 속성 개수와 도메인을 가져야만 한다.
| 명제로 표현하면 두 릴레이션 R1( A1, A2 ..An)과 R2( B1, B2, ... Bm)이 합집합 호환일때
필요충분 조건은 n = m, 모든 1 <= i <= n에 대해 domain(Ai) = domain(Bi)

1. 릴레이션끼리만 보면 애트리뷰트 수가 달라 호환이 되지 않는다.
2. 프로젝션 결과에서 π DEPTNO(DEP) == π DNO (EMP) 는 애트리뷰트 수가 같고, 두 컬럼의 도메인이 같으므로 합집합 호환이다.

Union ∪
- 중복 튜플은 제거된다.
- 차수는 R, S 둘 중 하나의 릴레이션과 같다.

Difference -
- 차수는 R, S 둘 중 하나의 릴레이션과 같다.
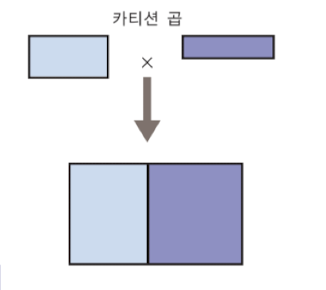
Cartesian Product x
- R, S 튜플의 모든 가능한 조합으로 이루어진 릴레이션이다. 결과 릴레이션이 너무 커서 이 자체로는 유용한 연산자가 아니다.
- 차수: n, m => n + m. Cardinality: i, j => i*/j
- Outer join과 다른 점은 null로 대체하지 않고 조합을 만든다는 점이다.
Relationally complete
임의의 질의어가 필수적인 관계 대수 연산자들만큼의 표현력을 가진 상태.
- 아래의 SQL 질의는 관계 대수의 Select, Join, Project 연산으로도 동일하게 표현되므로, SQL은 relationally complete합니다.
SELECT Course.수업명 FROM Student JOIN Course ON Student.학과 = Course.학과 WHERE Student.학과 = '컴퓨터공학';
유도된 관계 연산자
모든 관계 연산자는 필수 관계 연산자 두 개 이상의 조합으로 표현할 수 있다. 과정이 중복되고 계산식이 복잡하니까 한 번에 표현해놓은 '편의를 위한' 연산자
- 교집합 연산자 ∩
- 조인 연산자
- 세타 조인 ⋈θ , 동등 조인 ⋈ , 자연 조인 ⋈ N (*/) , 외부 조인 ⟗, 세미 조인 ⋉
- 디비전 연산자 ÷
교집합 연산자
두 릴레이션(테이블)에서 겹치는 부분을 뽑아내기 위해서 필수 연산자로는 π ( σ (TABLE)) 을 두 번 연산해서 × 하나의 테이블로 만든 다음 다시 π ( σ ())로 겹치는 내용만 추출해야 된다. 이는 마지막 과정을 ∩로 간략하게 표현할 수 있다.
예) john이 속한 기획부서의 부서번호를 검색하라
R1 <- π DNO ( σ EMPNAME = 'john'(EMPLOYEE))
R2 <- π DEPTNO ( σ DEPTNAME = '기획'(DEPARTMENT))
R3 <- R1 ∩ R2조인 연산자
두 개 이상의 릴레이션(테이블)을 다룰 때 매우 중요한 연산자이다. 조인 연산자가 많아서 뭐가 뭔지 헷갈릴 수 있지만 기본적으로는 어떤 조건에 맞게 튜플을 서로 다른 두 개 이상의 릴레이션에서 추출하는 과정이다. 가장 기본적으로 자연 조인이 자주 사용된다.



자연 조인
동등 조인 ⋈ ( = ) 에서 조인한 attribute 한 개를 제외한 값이다. 위 예제에서 두 릴레이션에서 deptno = dno 를 동등 조건으로 사용하면 생성되는 결과 릴레이션은 deptno, dno 중복된 값을 가지는 두 개의 컬럼을 가진다. 자연 조인에서는 앞에서 쓴 조건 deptno 만을 조인 애트리뷰트로 가진다.
즉, 동등 조인의 차수 = 자연 조인의 차수 + 1 , 그 외는 동일하다.
위에서 본 예제는 자연 조인으로 표현하면 EMPLOYEE * DNO, DEPTNO DEPARTMENT 로 하나의 결과 릴레이션으로 만들 수 있다. 그럼 위 예제는
π EMPNAME, DEPTNAME ( σ EMPNAME = 'john' AND DEPTNAME = '기획'(EMPLOYEE * DNO, DEPTNO DEPARTMENT))으로 표현할 수 있다.
- 세타 조인 ⋈θ
θ = { = , <>, <=, >=, >, < } - 동등 조인 ⋈ =
- 자연 조인 ⋈ N (*/)
- 외부 조인 ⟗
- 세미 조인 ⋉
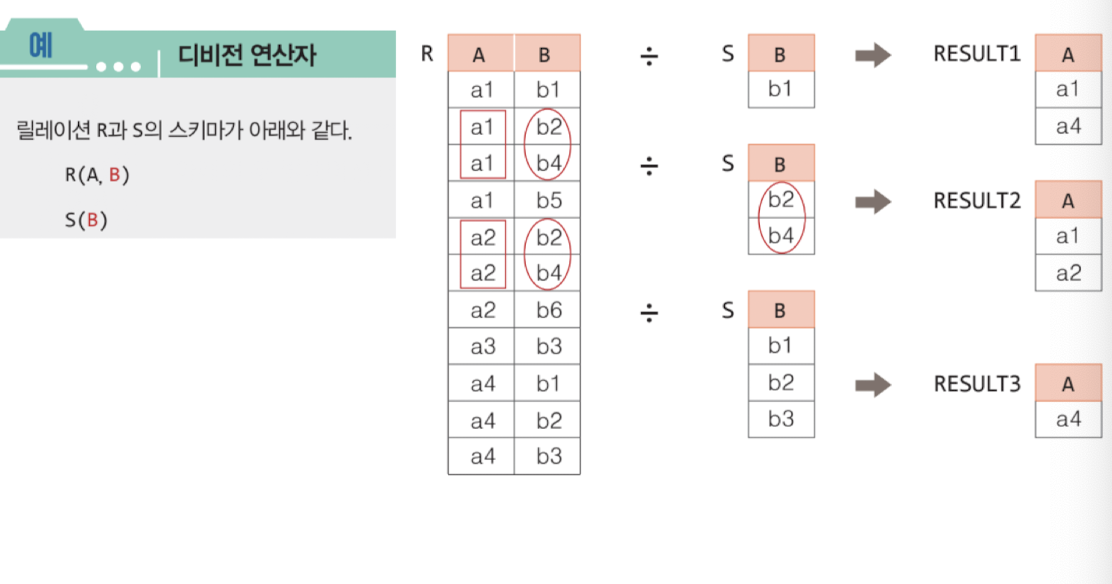
디비전 연산자 ÷
차수 n + m인 릴레이션R 에서 m개의 차수에서 가지는 값(S)을 포함한 집합을 보고 싶을 때, R ÷ S
이는 차수가 n이고, S가 속했던 튜플에서 뜯어낸 튜플을 집합으로 가진다.
- 이건 눈으로 봐야 한다...
관계 대수에서 selection, projection, join으로 거의 모든 연산이 가능하다.



관계 대수의 한계 및 추가된 관계 연산자
말이 넘 딱딱해서 의미가 직관적으로 와닿지가 않는다. 관계대수를 쓰다보니 이런 저런 점들이 안되더라.
이런 저런 점들에는 산술 연산이 되지 않아, 집단 함수(aggregate function)을 못 써, 정렬도 안 되고, 디비 수정도 안되고, 중복 투플을 나타낼 상황에 중복 투플을 나타낼 수 없는 상황들이 있더라.. 자 하나하나씩 살펴봅시다.
산술 연산이 되지 않아서 튜플의 최대, 최소값, 평균값을 구하지 못했다. 이를 나타내기 위해 집단 함수를 사용한다.
집단 함수(aggregate function)
aggregate: 종합하다. 라는 뜻인데 관련 객체(요소)들을 집합으로 묶어놓는다는 것이다. 그냥 여러 튜플을 사용해서 계산하겠다는 뜻이다.
- SUM, AVG, MAX, MIN, COUNT 등
- 각 부서별 사원들의 급여 평균은 얼마인가?
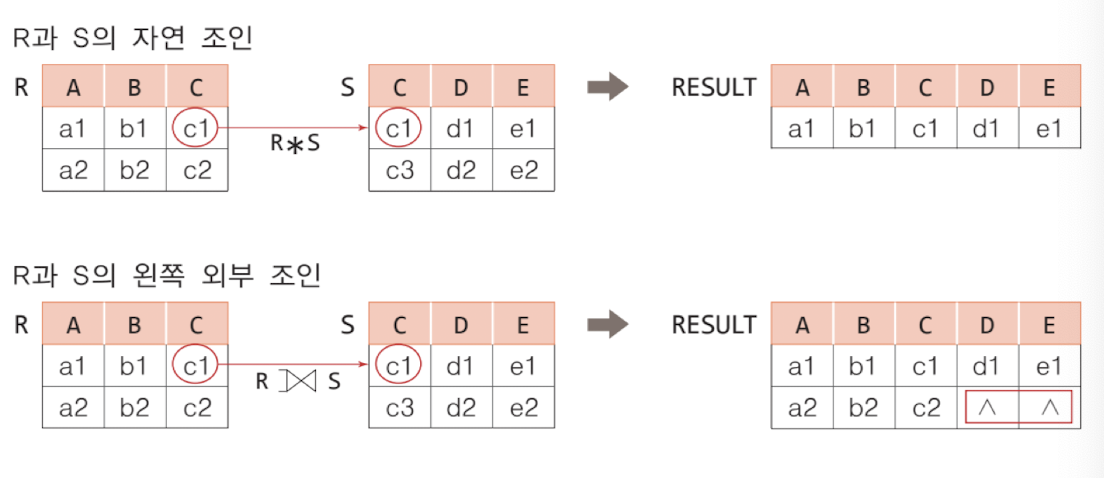
외부 조인 OUTER JOIN
조인 연산을 확장했다. 어떤 경우에는 대응되지 않아도 null로 표현되어야 할 상황이 있다. 이를 위해 join attribute에 null 값을 가지는 튜플도 포함시킨다.
- left outer join ⟕
- 왼쪽을 기준으로 오른쪽 친구를 불러와서 없는 값은 null로
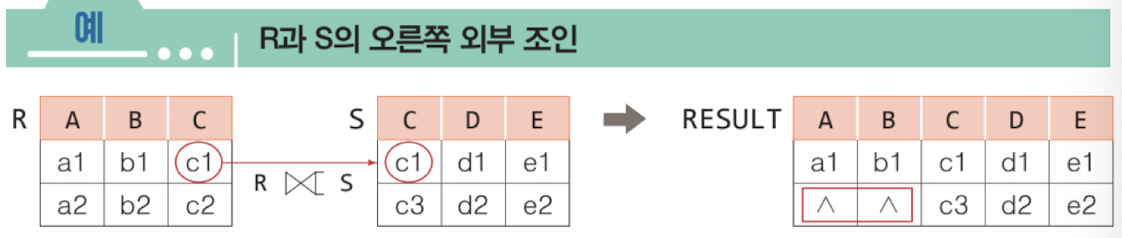
- right outer join ⟖
- full outer join ⟗
- 누락되는 값이 하나도 없게 채운다.

'Computer Science > DataBase' 카테고리의 다른 글
| [데이터베이스] 서브쿼리 (0) | 2025.03.08 |
|---|---|
| [데이터베이스] window 함수 (0) | 2025.03.08 |
| 관계 데이터 모델 기본 개념과 제약 조건 (3) | 2024.10.23 |
| [SQL] SELECT, INSERT, DELETE, UPDATE (4) | 2024.10.23 |
| [SQLD] 자료 사이트 정리 (0) | 2024.08.22 |




