CS/DataBase

[관계 대수] 관계 연산자

아란정 2024. 10. 23. 15:18

관계 대수 relational algebra

원하는 데이터를 어떠한 연산과 연산 순서로 가져오라고 명시하는 절차적인 언어. SQL의 이론적인 기초가 되는 언어다.
관계 DBMS는 SQL 질의를 DBMS 내부에서 관계대수식으로 변환한 후 최적의 질의 수행 계획을 찾는다.
우리는 DB에 SQL로 어떤 데이터를 달라고 명령하게 된다. 이 명령을 DBMS는 관계대수식으로 변환해서 연산을 수행하니 관계대수식을 알면 데이터 처리 방법에 대해 이해할 수 있다.

관계 데이터 모델에서 지원하는 두 가지 정형적인 언어

정형적인이 무슨 뜻 일까?

  • 관계 해석 relational calculus
    • 원하는 데이터만 명시
  • 관계 대수 relational algebra

필수 관계 연산자

Selection σ

  • selection의 조건을 predicate(술어)라고 한다.
  • 조건에는 애튜리뷰트, 상수, 비교 연산자 등의 bool 연산자를 포함할 수 있다.
  • 중복 튜플이 존재할 수 없다.

 

Projection π

  • 릴레이션 애튜리뷰트의 부분 집합; 결과에 쓸 컬럼을 쓰면 된다; 중복 튜플이 존재할 수 있다.

 

집합 연산자

  • UNION(∪), INTERSECTION(∩), DIFFERENCE(-)
    여기서 교집합만 유도 연산자다.

 

  • | 합집합 호환
    두 릴레이션은 서로 같은 속성 개수와 도메인을 가져야만 한다.
    | 명제로 표현하면 두 릴레이션 R1( A1, A2 ..An)과 R2( B1, B2, ... Bm)이 합집합 호환일때
    필요충분 조건은 n = m, 모든 1 <= i <= n에 대해 domain(Ai) = domain(Bi)

합집합 호환일까?

1. 릴레이션끼리만 보면 애트리뷰트 수가 달라 호환이 되지 않는다. 
2. 프로젝션 결과에서 π DEPTNO(DEP) ==  π DNO (EMP) 는 애트리뷰트 수가 같고, 두 컬럼의 도메인이 같으므로 합집합 호환이다. 

 

Union ∪

  • 중복 튜플은 제거된다.
  • 차수는 R, S 둘 중 하나의 릴레이션과 같다.

 

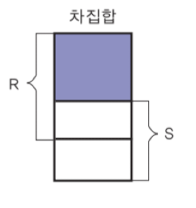
Difference -

  • 차수는 R, S 둘 중 하나의 릴레이션과 같다.

 

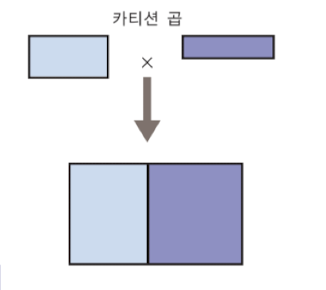
Cartesian Product x 

  • R, S 튜플의 모든 가능한 조합으로 이루어진 릴레이션이다. 결과 릴레이션이 너무 커서 이 자체로는 유용한 연산자가 아니다.
  • 차수: n, m => n + m. Cardinality: i, j => i*/j
  • Outer join과 다른 점은 null로 대체하지 않고 조합을 만든다는 점이다.

Relationally complete

임의의 질의어가 필수적인 관계 대수 연산자들만큼의 표현력을 가진 상태.

  • 아래의 SQL 질의는 관계 대수의 Select, Join, Project 연산으로도 동일하게 표현되므로, SQL은 relationally complete합니다.
  • SELECT Course.수업명 FROM Student JOIN Course ON Student.학과 = Course.학과 WHERE Student.학과 = '컴퓨터공학';

유도된 관계 연산자

모든 관계 연산자는 필수 관계 연산자 두 개 이상의 조합으로 표현할 수 있다. 과정이 중복되고 계산식이 복잡하니까 한 번에 표현해놓은 '편의를 위한' 연산자

  • 교집합 연산자 ∩
  • 조인 연산자
    • 세타 조인 ⋈θ , 동등 조인 ⋈ , 자연 조인 ⋈ N (*/) , 외부 조인 ⟗, 세미 조인 ⋉
  • 디비전 연산자 ÷

교집합 연산자

두 릴레이션(테이블)에서 겹치는 부분을 뽑아내기 위해서 필수 연산자로는 π ( σ (TABLE)) 을 두 번 연산해서 × 하나의 테이블로 만든 다음 다시 π ( σ ())로 겹치는 내용만 추출해야 된다. 이는 마지막 과정을 ∩로 간략하게 표현할 수 있다.

예) john이 속한 기획부서의 부서번호를 검색하라

R1 <- π DNO ( σ EMPNAME = 'john'(EMPLOYEE)) 
R2 <- π DEPTNO ( σ DEPTNAME = '기획'(DEPARTMENT))
R3 <- R1 ∩ R2

조인 연산자

두 개 이상의 릴레이션(테이블)을 다룰 때 매우 중요한 연산자이다. 조인 연산자가 많아서 뭐가 뭔지 헷갈릴 수 있지만 기본적으로는 어떤 조건에 맞게 튜플을 서로 다른 두 개 이상의 릴레이션에서 추출하는 과정이다. 가장 기본적으로 자연 조인이 자주 사용된다.

세타 조인: 세타는 비교 연산자다.
동등 조인은 세타가 = 일 때
자연조인은 동등 조인에서 조인 애트리뷰트 중복 하나 제거

자연 조인

동등 조인 ⋈ ( = ) 에서 조인한 attribute 한 개를 제외한 값이다. 위 예제에서 두 릴레이션에서 deptno = dno 를 동등 조건으로 사용하면 생성되는 결과 릴레이션은 deptno, dno 중복된 값을 가지는 두 개의 컬럼을 가진다. 자연 조인에서는 앞에서 쓴 조건 deptno 만을 조인 애트리뷰트로 가진다.
즉, 동등 조인의 차수 = 자연 조인의 차수 + 1 , 그 외는 동일하다.

위에서 본 예제는 자연 조인으로 표현하면 EMPLOYEE * DNO, DEPTNO DEPARTMENT 로 하나의 결과 릴레이션으로 만들 수 있다. 그럼 위 예제는

 π EMPNAME, DEPTNAME ( σ EMPNAME = 'john' AND  DEPTNAME = '기획'(EMPLOYEE * DNO, DEPTNO DEPARTMENT))

으로 표현할 수 있다.

  • 세타 조인 ⋈θ
    θ = { = , <>, <=, >=, >, < } 
  • 동등 조인 ⋈ =
  • 자연 조인 ⋈ N (*/)
  • 외부 조인 ⟗
  • 세미 조인 ⋉

디비전 연산자 ÷

차수 n + m인 릴레이션R 에서 m개의 차수에서 가지는 값(S)을 포함한 집합을 보고 싶을 때, R ÷ S
이는 차수가 n이고, S가 속했던 튜플에서 뜯어낸 튜플을 집합으로 가진다.

  • 이건 눈으로 봐야 한다...

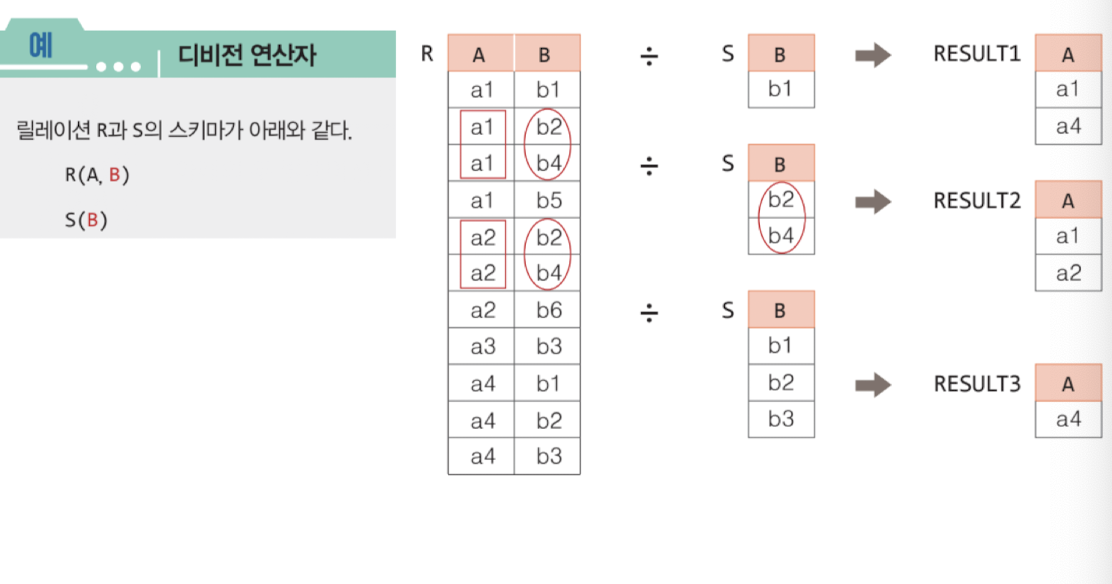
관계 대수에서 selection, projection, join으로 거의 모든 연산이 가능하다.

 

관계 대수 - 조인을 이해하기 좋은 퀴즈

관계 대수의 한계 및 추가된 관계 연산자

말이 넘 딱딱해서 의미가 직관적으로 와닿지가 않는다. 관계대수를 쓰다보니 이런 저런 점들이 안되더라.
이런 저런 점들에는 산술 연산이 되지 않아, 집단 함수(aggregate function)을 못 써, 정렬도 안 되고, 디비 수정도 안되고, 중복 투플을 나타낼 상황에 중복 투플을 나타낼 수 없는 상황들이 있더라.. 자 하나하나씩 살펴봅시다.

산술 연산이 되지 않아서 튜플의 최대, 최소값, 평균값을 구하지 못했다. 이를 나타내기 위해 집단 함수를 사용한다.

집단 함수(aggregate function)

aggregate: 종합하다. 라는 뜻인데 관련 객체(요소)들을 집합으로 묶어놓는다는 것이다. 그냥 여러 튜플을 사용해서 계산하겠다는 뜻이다.

  • SUM, AVG, MAX, MIN, COUNT 등
  1. 각 부서별 사원들의 급여 평균은 얼마인가?

외부 조인 OUTER JOIN

조인 연산을 확장했다. 어떤 경우에는 대응되지 않아도 null로 표현되어야 할 상황이 있다. 이를 위해 join attribute에 null 값을 가지는 튜플도 포함시킨다.

  • left outer join ⟕
    • 왼쪽을 기준으로 오른쪽 친구를 불러와서 없는 값은 null로
  • right outer join ⟖
  • full outer join ⟗
    • 누락되는 값이 하나도 없게 채운다.

저작자표시 비영리 변경금지